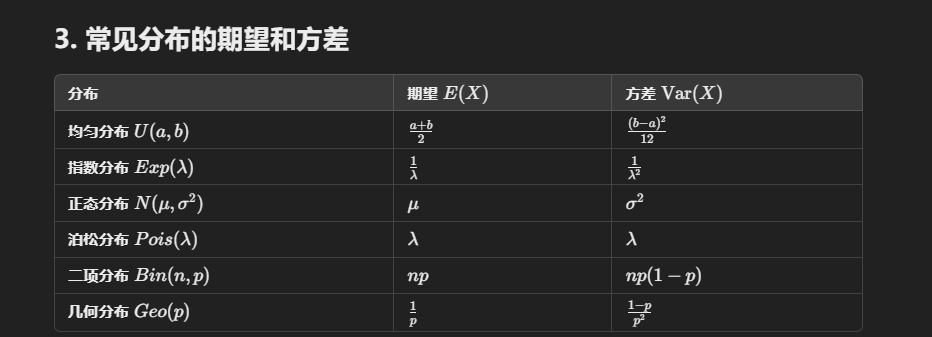
# 重要知识点梳理

# 五种重要的分布

# 1. 二项分布（Binomial Distribution）

定义

• 适用于独立重复伯努利试验（每次试验只有成功或失败两种情况）。
• 统计成功次数。

参数

• X∼Bin(n,p)$$其中： - n是试验次数。 - p是单次试验成功的概率。

$$P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}, \quad k = 0,1,2,\dots,n$$

其中，$$\binom {n}{k} = \frac {n!}{k!(n-k)!}$$ 是组合数。

性质

• 期望（均值）：E(X)=np
• 方差：Var (X)=np (1−p)
• 应用场景：
  • 投掷 n 次硬币，统计正面出现的次数。
  • 在 100 个产品中，计算有缺陷产品的数量（假设每个产品的缺陷概率是 p）。
  • 在一次市场调查中，计算支持某个品牌的顾客数量。

# 2. 泊松分布（Poisson Distribution）

定义

• 适用于单位时间或单位空间内，独立随机事件的发生次数。
• 例如：某个银行 1 小时内接到的客户电话数量。

参数

• X∼Pois (λ)，其中 λ 是单位时间 / 空间内的平均发生次数。

概率质量函数（PMF）

$$P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}, \quad k = 0,1,2,...$$

性质

• 期望：E (X)=λ
• 方差：Var (X)=λ
• 泊松近似：当 n 很大、p 很小（np=λ），二项分布可用泊松分布近似：$$Bin (n,p)≈Pois (λ)$$

应用场景

• 单位时间内的电话呼入数量。
• 单位面积内的细菌数。
• 交通流中每分钟通过某点的车辆数。

# 3. 均匀分布（Uniform Distribution）

定义

• 适用于在区间 [a,b] 内，每个值的概率完全相同。
• 分为离散和连续两种情况，我们这里讲连续均匀分布。

参数

• X∼U (a,b)，即 XXX 在区间 [a,b] 内均匀分布。

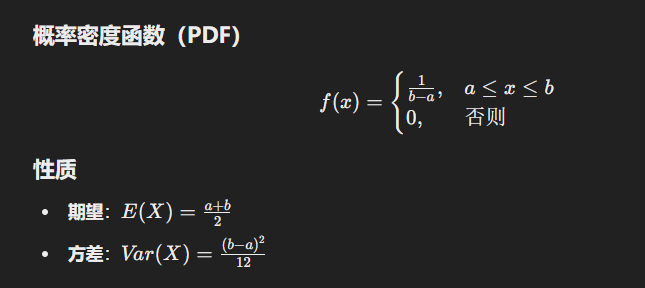
应用场景

• 随机生成一个 0 到 1 之间的随机数（计算机通常用均匀分布生成伪随机数）。
• 随机选择某个时间点（假设在某个时间段内，每个时间点的概率相同）。
• 在模拟实验中，生成随机数据。

# 4. 指数分布（Exponential Distribution）

定义

• 适用于事件发生的时间间隔。
• 例如：两次客户电话呼入之间的时间间隔。

应用场景

• 电话呼入的时间间隔。
• 电子元件的寿命（假设故障率恒定）。
• 地震发生的时间间隔。

# 5. 正态分布（Normal Distribution）

定义

• 适用于自然界和社会现象中的大量数据，如身高、体重、考试成绩等。

应用场景

• 人的身高、体重、智商分数等。
• 误差分析：测量误差和噪声往往服从正态分布。
• 金融市场收益的近似分布。

# 全概率公式与贝叶斯公式

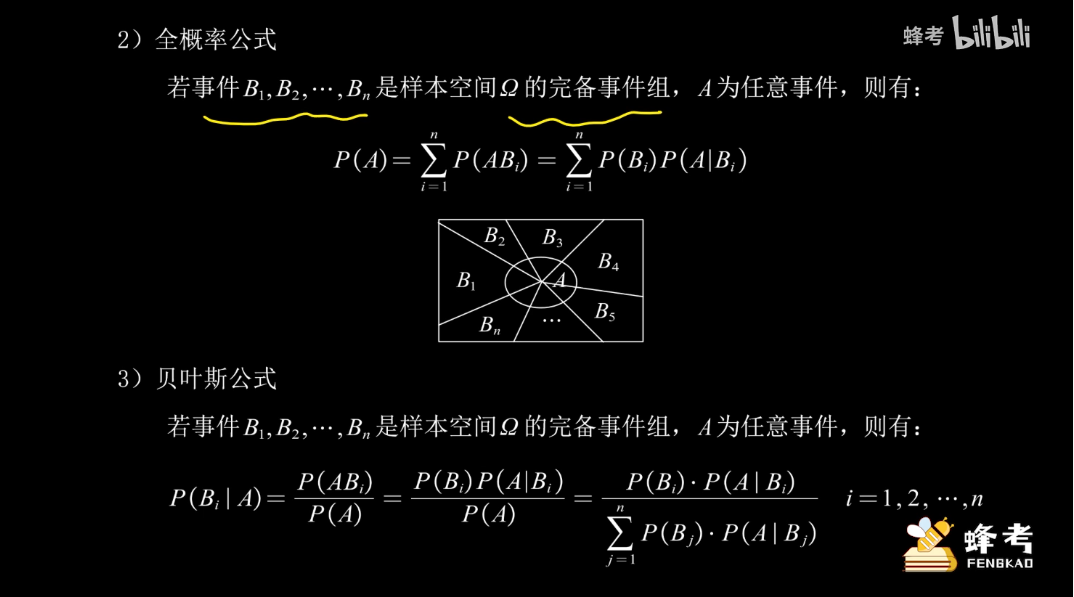
# 一维连续型随机变量及定义

# 期望与方差

1. 期望
   
   

2. 方差
   
   

3. 常见期望与方差
   

# 一些定理

# 切比雪夫定理

# 一些符号的含义

1. 上界与下界
   ✅ 一、$O(\cdot)$ —— 大 O 符号（上界）
   含义：

最多有多快增长
表示函数的增长速度 不会超过某个量级

举个例子：
$f(n) = 3n + 5 = O(n)$
意思是：当 n 很大时，f (n) 的增长速度最多就像 n 这样。

✅ 二、$\Omega(\cdot)$—— 大 Ω 符号（下界）
含义：

至少有多快增长
表示函数的增长速度 最小不会低于某个量级

举个例子：
$f(n) = 3n + 5 = \Omega(n)$
意思是：f (n) 至少会像 n 一样快增长，不可能比它慢太多。

# 📚 二项式展开公式（Binomial Theorem）

# 🎯 公式内容

对于任意整数 $n \geq 0$，都有：

[
$(1 + x)^n = \sum_{k=0}^{n} \binom{n}{k} x^k$
]

即：

[
$(1+x)^n = \binom{n}{0}x^0 + \binom{n}{1}x^1 + \binom{n}{2}x^2 + \cdots + \binom{n}{n}x^n$
]

其中：

• $\binom{n}{k}$ 是组合数，表示 “从 $n$ 个元素里选 $k$ 个的方式数”，公式为：
  [
  $\binom{n}{k} = \frac{n!}{k!(n-k)!}$
  ]

# ✏️ 小例子

# 当 $n = 2$ 时：

[
$(1+x)^2 = 1 + 2x + x^2$
]

展开过程：

• $\binom{2}{0}x^0 = 1$
• $\binom{2}{1}x^1 = 2x$
• $\binom{2}{2}x^2 = 1x^2$

# 当 $n = 3$ 时：

[
$(1+x)^3 = 1 + 3x + 3x^2 + x^3$
]

展开过程：

• $\binom{3}{0}x^0 = 1$
• $\binom{3}{1}x^1 = 3x$
• $\binom{3}{2}x^2 = 3x^2$
• $\binom{3}{3}x^3 = x^3$

# 💡 更一般的形式

对于一般的 $(a+b)^n$：

[
$(a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k$
]

特点：

• 每一项中 $a$ 和 $b$ 的指数之和为 $n$；
• 系数是组合数 $\binom{n}{k}$。

# ✅ 在应用中的例子

如果展开 $(1-p)^k$，就是将 $x$ 换成 $-p$：

[
$(1-p)^k = \sum_{\ell=0}^{k} \binom{k}{\ell} (-1)^\ell p^\ell$
]

• 其中每项有符号变化 $(-1)^\ell$。

# 📋 小结

# 📚 泰勒展开（Taylor Series）总结笔记

# 🎯 什么是泰勒展开？

泰勒展开是一种用多项式（无穷级数）来近似描述一个光滑函数的方法。

简单说：

• 把函数 $f(x)$ 在某点（通常是 $x=0$ 或其他 $a$）附近，
• 用一次项、二次项、三次项…… 无限多项式的方式来逼近表达，
• 每一项和函数在那个点的导数值有关。

# ✅ 泰勒展开公式

如果函数 $f(x)$ 在点 $a$ 处有无穷多个连续导数，那么：

[
$f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \cdots$
]

也可以用求和写成：

[
$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n$
]

• $f^{(n)}(a)$ 表示函数在 $a$ 点处的第 $n$ 阶导数；
• $n!$ 是 $n$ 的阶乘。

# 🛠️ 特别情况：Maclaurin 展开

如果选择 $a = 0$，泰勒展开就变成了 Maclaurin 展开：

[
$f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \cdots$
]

# ✏️ 常见例子

# 1. 指数函数 $e^x$ 的展开

[
$e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots$
]

# 2. 正弦函数 $\sin(x)$ 的展开

[
$\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots$
]

• 注意奇次幂、正负号交替。

# 3. 余弦函数 $\cos(x)$ 的展开

[
$\cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots$
]

• 偶次幂、正负号交替。

# 💡 直观理解

• 低阶展开（只取前几项）给出粗略近似；
• 多取几项，展开多项式的近似效果越来越好；
• 是分析复杂函数、小扰动分析、算法近似估计的重要工具。

# 📋 小总结表

# 等比数列求和公式

# ✅ 有限项求和公式

如果你只求前 (n) 项（从第 0 项到第 ( n-1 ) 项），总和是：

[
$S_n = a\frac{1 - r^n}{1 - r} \quad \text{（当 } r \neq 1\text{）}$
]

• 适用于 ($r \neq 1$ )
• (S_n) 是前 ( n ) 项的总和

# ✅ 无限项求和公式

当 (|r| < 1) 时，等比数列可以无限加下去，并且求和收敛。

无穷求和公式是：

[
$S = \frac{a}{1 - r}$
$\quad \text{（当且仅当 } |r| < 1 \text{）}$
]

• (a) 是首项
• (r) 是公比
• 注意：如果 (|r| \geq 1)，这个和就发散了（不会收敛）。

# 📚 常用数学术语英文总结

# 🔵 基本性质类

# 🔵 概率与不等式类

# 🔵 公式与操作类

# ✨ 小总结

简单理解：
increasing ➔ 变大，bounded ➔ 不爆炸，converge ➔ 趋向稳定，concentration ➔ 不乱跑！

# 📚 常见数学符号速查表

# 🔵 运算符号类

# 🔵 逻辑符号类

# 🔵 概率统计符号类

# 🔵 集合相关符号

# 📐 范数（Norm）总结笔记

范数是一种用于度量向量 “大小” 或 “距离” 的数学工具，在流式算法、机器学习和信号处理等场景中广泛使用。

# ✅ 常见范数定义

# 1. L₁ 范数（曼哈顿距离 / 稀疏性度量）

1

‖x‖₁ = |x₁| + |x₂| + ... + |xₙ|

• 含义：所有元素绝对值之和
• 应用：误差总量、频率总和、稀疏性建模

# 2. L₂ 范数（欧几里得范数 / 能量）

1

‖x‖₂ = √(x₁² + x₂² + ... + xₙ²)

• 含义：向量长度（直线距离）
• 应用：最小二乘法、波动性、能量度量

# 3. L∞ 范数（最大范数）

1

‖x‖∞ = max(|x₁|, |x₂|, ..., |xₙ|)

• 含义：向量中最大绝对值
• 应用：控制最大误差，最坏情况分析

# 4. L₀ “范数” （非零项计数）

1

‖x‖₀ = 向量中非零元素的个数

• 注意：严格来说它不是数学意义上的范数
• 应用：统计不同元素个数、稀疏建模

# 📏 范数之间的大小关系

1

‖x‖∞ ≤ ‖x‖₂ ≤ ‖x‖₁

• L∞ 控制最坏情况；
• L₂ 衡量整体波动；
• L₁ 是 “总量”。

# 🧠 与 Sketch 的关系

在流式算法中：

• 数据流被表示成频率向量 f ∈ ℝⁿ
• 范数用来衡量 sketch 与真实向量之间的误差
• 常见误差控制：
  • ‖f - f̂‖₁ ≤ ε‖f‖₁
  • ‖f - f̂‖∞ ≤ ε‖f‖₁
  • ‖f - f̂‖₂ ≤ ε‖f‖₂

# 🧾 示例类比

若向量 x = [3, -2, 4] ：