lec9 Planar Point Location

# 1. 平面点定位问题

首先代入日常生活，就如同我们使用地图软件一般，我们点击某个点的时候，我们需要快速判断出我们点的是哪个区间的点。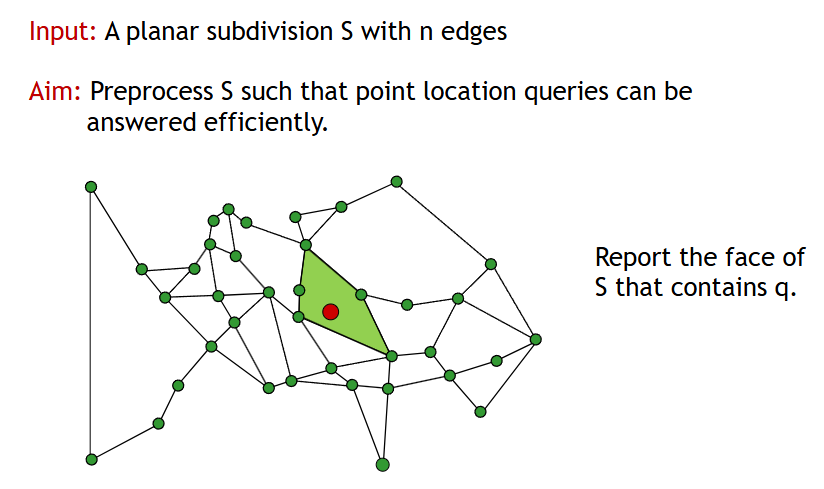

自然而然的可以想到的就是暴力法，即每次搜索点的时候都通过线性扫描扫描所有的点，但是这样的效率太低了，每次都需要 O (n) 的时间复杂度，所以接下来我们考虑别的方式

# 1.1 垂直切分法（Vertical Slab Decomposition）

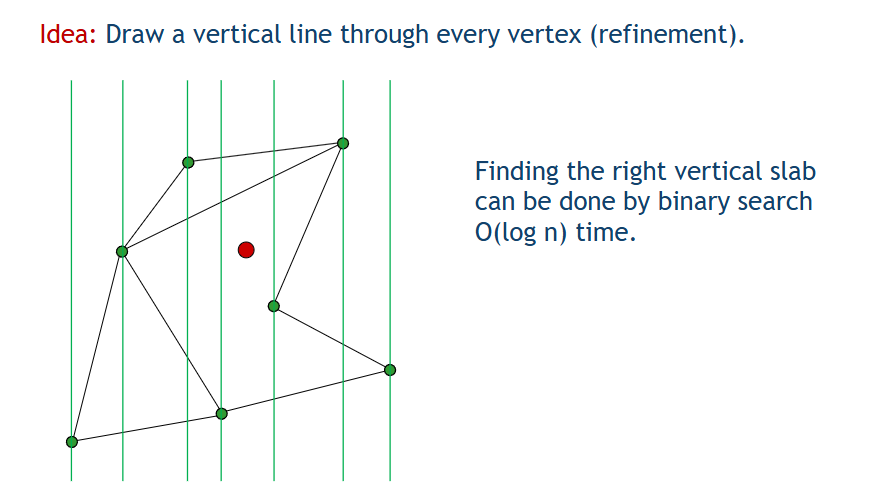
如图所示，我们可以按照每个点所在的 y 轴进行切分，然后根据二分查找，第一次找出点所在的 slab。
然后，找出在哪个 slab 后，我们可以再进行一次二分查找，从而找到点在哪两个线段之间。
因此，我们的时间复杂度为 O (log n)
但是因此我们也碰到了一个问题：空间复杂度
每个 slab 理论最多有 O (n) 个线段，而理论上最多有 O (n) 个 slab
因此，最多空间为 O (n^2)，这太大了

# 1.2 随机增量构建（RIC）

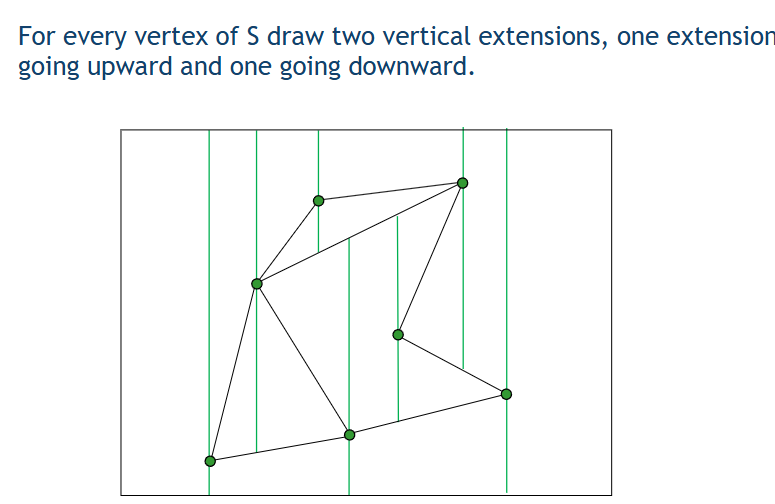
首先，我们将所有的点都放在一个平面中，然后所有点都向上下射出一条射线；
然后，随机依次将线段添加进平面当中，只需要判断添加这条线段后影响了多少梯形 / 三角形即可，不需要遍历所有的空间。
因此这样的空间和时间复杂度都不会太高；

接下来，我们开始构建这个数据结构：
使用 DAG，即有向无环图
可以将他构建成一个易于搜索的树结构
而在这个树当中，存在 X-node 和 y-node，每个 x-node 通过 x 来判断接下来搜索需要向左还是向右；
而 y-node 是一个线段，通过判断这个点在线段上方还是下方来判断接下来需要往上走还是往下走；
最终会到叶子节点 —— 即树的最底端，一个个梯形，则得到需要搜索的点在哪个位置。
而在添加新的线段时，就会需要先查询位于这个树的哪个位置，然后根据位置进行替换，将这块的新的数据结构替换原本的。

整个过程的时间复杂度就是构建这个树的复杂度和搜索的复杂度

# 正确性分析：

T (s_i): 用于存储前 i 条线段生成的梯形图
D (s_i): 用于存储前 i 条线段生成的搜索结构
那么我们可以把一开始的结构看成是一个空的图，即 T 中是一个空的图，D 中是仅仅只有这张图的叶子节点
当我们插入一条新的线段的时候，这个图会被分成新的梯形，因此被这个新的线段穿过的所有梯形都不会在新的 T 和 D 中存在，取而代之的是因为穿过而产生的新的梯形，并且由于每次插入新的线段时都会进行这样的操作，每次都会确保正确，因此到所有线段都插入结构时，结构也是正确的。
通俗来理解，可以看作是搭乐高积木，我们的每一步都搭对了，那么最终的结果也是对的。

如何寻找被 s_i 插入的新梯形？
更改 T
我们从新插入线段的一个端点开始，依次移动，并移动到下一个端点，记录过程中穿过的所有梯形。现在我们就知道了我们的 zone，即所有需要更改的梯形，将他们从原有的结构中移除，并插入所有的新的梯形。
更改 D
与 T 类似，我们需要把所有底端的需要移除的叶子节点，即梯形移除，并在原本位置上插入新的小 DAG，代表新生成了几个梯形。因此这样可以确保从查询过程最终仍然会走到叶子节点，确保了结构的正确性。

那么查询会不会出错呢？
因为我们每次的修改只更改需要修改的 zone。所以如果查询点 p 所在的梯形没有被穿过的话， 那么久不需要更改搜索路径，搜索的路径不会发生改变。
而 p 所在的梯形被穿过了，那么我们会用新的小的 DAG 来替换原本的梯形，确保仍然会有新的最终的叶子节点，因此原本旧的路径会重新指向新的梯形，即叶子节点。所以也能确保正确性。

# 复杂度分析：

# 期望查询时间复杂度：

我们希望得到期望的查询时间复杂度，我们可以通过求整个插入线段的过程中的平均路径长度来得到
我们设：

• $X_i$：表示第 $i$ 次插入线段时，是否向查询路径中新增了一个节点；
• $E[\sum X_i]$：就是我们最终想要的 “期望路径长度”。
  这里我们运用了反向分析：即如果我们要删除一条边的时候，某个固定的梯形 T_i 是否会因为这条线段的移除而消失
  由于每次删除一条线段的时候，梯形由四条边构成，所以某个梯形会受到影响的概率为 4/i

$$P_i \le \frac{4}{i}$$

由于可以假定每个 DAG 结构都是由三层构成，即 3 层为下界，我们可以保守估计

$$\mathbb{E}[X_i] \le 3 \cdot P_i \le \frac{12}{i}$$

所以问题就转换成了
代入后我们得到：

$$\mathbb{E}\left[\sum X_i\right] \le \sum_{i=1}^n \frac{12}{i}$$

这就是著名的调和级数，我们知道它是：

$$\sum_{i=1}^n \frac{1}{i} = \ln n + \gamma \approx O(\log n)$$

所以最终：

$$\mathbb{E}\left[\sum X_i\right] = O(\log n)$$

# 构建空间复杂度：

分析过程与查询时间一致，但是
实际上：

• 插入任意一条线段，它平均只穿过 $O(1)$ 个梯形（经过分析）；
• 每条线段生成的梯形个数期望是常数；

所以所有线段插入后的总期望空间是：

$$O(n)$$

# 构建时间复杂度

由于构建的过程中，每次插入一条新的线段的过程如下

1. 查询需要插入的位置，由第一部分可得知复杂度为 O (log n)
2. 查询后删除和添加新的 DAG，由于每次删除和添加的 DAG 数量都为常数级，所以这部分为 O (1)

因此添加第 i 条线段的时间为 T_i = O (log i) + O (1) = O (log i)
所以期望时间为：
我们知道 $E[k_i] = O(1)$，所以：

$$\mathbb{E}[T_i] = O(\log i)$$

加总所有 $n$ 条线段的插入成本：

$$\sum_{i=1}^n \mathbb{E}[T_i] = \sum_{i=1}^n O(\log i) = O(n \log n)$$